Otomata & Teori Bahasa

EKIVALENSI

NON-DETERMINISTIC FINITE AUTOMATA

KE DETERMINISTIC FINITE AUTOMATA

Dari sebuah mesin NFA dapat dibuat mesin DFA-nya yang ekivalen (bersesuaian). Ekivalen disini artinya mampu menerima bahasa yang sama. Lihat FSA pada gambar 1 dan gambar 2. Gambar 1 adalah DFA sedangkan gambar 2 adalah NFA. Meskipun yang satu DFA dan yang lainnya NFA, kedua-duanya menerima bahasa yang sama, yang dalam ekspresi regular = 0 (0 U 1)*

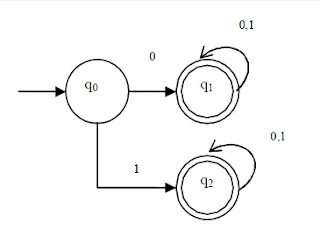GB 1. Mesin DFA

GB 2. Mesin NFA

GB 3. Mesin automata NFA

Tahapan Pengubahan

Sekarang kita lihat bagaimana membuat suatu DFA yang ekivalen dengan sebuah NFA. Misalkan kita ingin membuat mesin DFA dari mesin NFA pada gambar 3. 

• Pertama-tama yang kita lakukan adalah membuat table

transisi NFA tersebut. Bila diketahui ∑ = {0,1}, maka table transisinya adalah:

∂	0	1
q0	{q0,q1}	{q1}
q1	ᴓ	{q0,q1}

Dengan adanya table transisi tersebut akan mempermudah kita melakukan langkah selanjutnya. Kita akan mulai dari state awal, kemudian mengikuti transisinya untuk membentuk state-state baru, untuk setiap state yang terbentuk diikuti lagi transisinya sampai ter’cover’ semua. Berikut adalah Gambar hasil dari pengubahan NFA ke DFA

Hasil setelah penelusuran {q0} dan {q0, q1}

*Perhatikan state q1 menerima input 0 menjadi state ᴓ, disini ᴓ kita gambarkan juga sebagai sebuah state. Selanjutnya kita lihat semua state sudah kita telusuri/runut, tinggal state ᴓ. State ᴓ menerima input 0 atau 1 menjadi state ᴓ, atau  δ (ᴓ,1)= ᴓ. Hasilnya dapat kita lihat pada gambar ini.

Hasil setelah semua di telusuri

Kita ingat pada mesin NFA semula, himpunan state akhir adalah {q1}, maka pada DFA hasil perubahannya state-state akhir adalah semua state yang mengandung {q1}. Maka state akhirnya sekarang adalah state {q1} dan state {q0, q1} , atau secara formal: F={{q1},{q0, q1}}

Mesin DFA yang ekivalen dengan NFA pd gambar no 3

Kita bisa memeriksa apakah kedua otomata tersebut ekivalen. Untuk membuktikannya kita perlu memperlihatkan bahwa suatu bahasa yang diterima oleh NFA juga diterima oleh DFA ekivalennya tersebut. Bila diketahui NFA semula gambar menerima string ‘001’, maka seharusnya DFA pada gambar juga menerima string tersebut. Kita lihat : δ (q0,001) =δ({q0, q1},01)= δ ({q0, q1},1)= {q0, q1} Karena state {q0, q1} termasuk state akhir, maka berarti string tersebut diterima.